Do Plano Cartesiano aos Gráficos

Vamos começar nosso assunto de hoje estudando o mapa abaixo.

1)  Observe a planta de um clube desenhada em uma malha quadriculada e responda às questões.

     Como você faria o seguinte trajeto: sair da quadra de tênis, passar pela piscina, pelo vestiário masculino(a) e entrar no ginásio de esportes. Como você poderia descrever esse caminho usando as coordenadas? Para organisarmos as respostas, vamos combinar que o primeiro número a ser escrito será o da linha horizontal combinado na sequência com outro da vertical, para indicar a localização de cada etapa do percurso.

2) Observe a localização de alguns lugares que estão apresentados na malha quadriculada e responda às questões.

a) Que logradouro está localizado em cada um destes pares ordenados?

( 1 ; 3 ) _____________________

( 8 ; 1 ) _____________________

( 4 ; 4 ) _____________________

b) Que par ordenado corresponde a cada um destes logradouros?

Clube  (     ;     )        

Escola (     ;     )        

Banco (     ;     )

     De maneira lúdica, e ainda podendo lembrar dos programas de televisão que usavam essa estratégia como jogos de batalha naval, começamos a trabalhar as coordenadas cartesianas.

     Podemos agora ir para a SAI (Sala Ambiente de Informática) para realizar algumas ATIVIDADES INTERATIVAS no Excel. Clique na imagem abaixo para interagir de maneira prática e dinâmica com esse problema ou outros que desejar acrescentar.

Na primeira atividade vamos poder trabalhar com duas cores e dispor 15 pontos de cada cor, simplesmente alterando as coordenadas cartesianas nas suas respectivas cores podendo assim observar de maneira mais prática, dinâmica os resultados dos conceitos aplicados e se apropriarem deles.

     Clique na imagem abaixo para interagir de maneira prática e dinâmica com esse problema ou outros que desejar acrescentar.


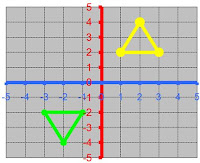     Nessa segunda atividade agora com mais conhecimento e habilidades, o objetivo seria ir para um segundo estágio, mais avançado onde organizados em dupla, um aluno escolhe um quadrante e cria um desenho e o outro por simetria deve reprodusir a imagem em um outro quadrante escolhido pelo desafiante para reporduzir a sua imagem, conforme o exemplo ao lado.

    Na sequência podemos fazer um trabalho de pesquisa histórico sobre René Descartes, para na próxima aula todos trazerem informações para um debate em sala de aula.

     O Sistema de Coordenadas Cartesianas, mais conhecido como Plano Cartesiano, foi criado por René Descartes (em pintura de Frans Hals) com o objetivo de localizar pontos.

     Filósofo e matemático francês nascido em 1596, René Descartes, é um personagem de destaque. A importância e representatividade de Descartes foi potencializado após a publicação do "Discurso sobre o Método", em 1637, no qual apresenta sua crença na caracterização do problema do método como garantia para a obtenção da verdade.

     Segundo o racionalismo de Descartes, o melhor caminho para a compreensão de um problema é a ordem e a clareza com que processamos nossas reflexões. Um problema sempre será mais bem compreendido se o dividirmos em uma série de pequenos problemas que serão analisados isoladamente do todo. Este fato leva até mesmo nossos dicionários acusarem um substantivo e um adjetivo em referências ao seu nome: cartesianismo e cartesiano.

     Descartes utilizou o terceiro capítulo de sua obra para a descrição de um tratado geométrico com os fundamentos daquilo que conhecemos hoje por geometria analítica, realizado com a intenção de ilustrar o alcance do método filosófico para o raciocínio e a busca da verdade.

     Em artigo sobre René Descartes, no site Consciência.org, disponível em  http://www.consciencia.org/descartes.shtml, podemos constar o fato que levou Descartes a finalizar seu tratado.

     O Plano Cartesiano é formado por dois eixos perpendiculares: um horizontal e outro vertical que se cruzam na origem das coordenadas. O eixo horizontal é chamado de abscissa (x) e o vertical de ordenada (y). Os eixos são enumerados compreendendo o conjunto dos números reais. Observe a seguir uma figura representativa do plano cartesiano:

     As coordenadas cartesianas são representadas pelos pares ordenados (x ; y). Em razão dessa ordem, devemos localizar o ponto observando primeiramente o eixo x e posteriormente

o eixo y. Qualquer ponto que não se encontrar sobre os eixos, estará localizado nos quadrantes, veja:

Os quatro quadrantes. O ponto A está no primeiro quadrante.

1º quadrante = x > 0 e y > 0
2º quadrante = x < 0 e y > 0
3º quadrante = x < 0 e y < 0
4º quadrante = x > 0 e y < 0

Localizando pontos no Plano Cartesiano:

A(4 ; 3) → x = 4 e y = 3

B(1 ; 2) → x = 1 e y = 2

C( –2 ; 4) → x = –2 e y = 4

D(–3 ; –4) → x = –3 e y = –4

E(3 ; –3) → x = 3 e y = –3

     O Plano Cartesiano é muito utilizado na construção de gráficos de funções, onde os valores relacionados à x constituem o domínio e os valores de y, a imagem da função. A criação do Sistema de Coordenadas Cartesianas é considerada uma ferramenta muito importante na Matemática, facilitando a observação do comportamento de funções em alguns pontos considerados críticos.

     Os movimentos cursor na tela do computador, os movimentos do mouse na mesa, são outros exemplos bem contextualizados que o plano cartesiano ajudou a desenvolver, para o prazer no uso do computador pelos jovens digitais.

     Podemos ainda associar o Plano Cartesiano com a latitude e a longitude, temas relacionados aos estudos geográficos e à criação do atual sistema de posicionamento, o GPS. O Sistema de Posicionamento Global permite que saibamos nossa localização exata na terra, desde que tenhamos em mão um receptor de sinais GPS, informando a latitude, a longitude e a altitude com o auxilio de satélites em órbita da Terra. Um exemplo de utilização do GPS são os aviões, que para não se colidirem são monitorados e informados em qual rota que devem seguir viagem.

     Vamos agora dar mais um passo nesse nosso estudo usando o Plano Cartesiano em outra situação cotidiana muito importante na vida dos nossos educando, os estudos da Função do 1º Grau.

O desafio dos alunos é o seguinte:

     Vai acontecer uma festa na escola e os alunos do 9º ano estão se organizando para construir uma tabela de preços para facilitar os trabalhos na barraca de pipoca. O lucro será de 100% uma vez que arrecadaram na comunidade escolar e no comércio todos os ingredientes e embalagens.

     Sabendo que um pacotinho de pipoca será vendido pelo valor de R$ 3,00 montaram a seguinte tabela:

     Com esse trabalho começaram a perceber que já poderiam ir além, prevendo o lucro obtido no final da festa, estimando certa quantidade vendida e seu respectivo resultado financeiro.

     Estava assim dado o início dos trabalhos de FUNÇÃO DO 1º GRAU já construindo paralelamente a tabela com os pares ordenados ( x ; y ).

     Aproveitando os conhecimentos do professor e dos alunos, voltamos a SAI para por em prática essas idéias. Clique na imagem abaixo para interagir de maneira prática e dinâmica com esse problema ou outros que desejar acrescentar.

Orientações da Planilha dessa atividade.

     Ela está protegida em suas configurações vitais para ajudar no rendimento dessa atividade, evitando possíveis acidentes com alterações indesejáveis, sendo o gráfico e a tabela.

      São liberados para modificações, apenas os títulos das tabelas, os valores de (X) e as fórmulas de (Y) que também podem ser trabalhadas como calculo mental digitando diretamente seus resultados.

     Alterando valores ou mesmo adequando outros problemas de forma contextualizada. Pode ainda explorar ainda situações crescente e decrescente, os coeficientes angular a(x) e linear b, as funções constantes, lineares e afins de ax + b = y. Em fim praticar com essa planilha pode ajudar alunos e professores em uma aula diferente e mais atualizada.

     Na sequência podemos incrementar o plano cartesiano acrescentando mais um termo nessa expressão algébrica, o X² e teremos a FUNÇÃO DO 2º GRAU.

     A equação na sua forma reduzida fica: ax² + bx + c = y

     Esse será o nosso estudo na sequência, enquanto isso aproveite a planilha para investigar e descobrir algumas propriedades dessa função:

     Clique na imagem abaixo para interagir de maneira prática e dinâmica com esse problema ou outros que desejar acrescentar.

Até as próximas aulas.